1111111...111という、1が延々と続く数を想像していただきたい。具体的には、136,279,841個の1が一列に並んでいる。これほど多くの枚数の紙を積み重ねると、それは塔となり、成層圏まで伸びていく。

この数をコンピューターに2進法（1と0のみを使用）で書き込むと、約16メガバイトでしかなく、短いビデオクリップ程度にしかならない。一般的な10進法表記に変換すると、この数は8,816,943,275...から始まり、...076,706,219,486,871,551で終わる、4100万桁以上になる。1冊の本ならば2万ページに相当する。

この数を別の方法で表記すると、2^136,279,841-1となる。この数にはいくつか特別な点がある。

第1に、この数は素数である（つまり、その数と1でしか割り切れない）。第2に、この数はメルセンヌ素数と呼ばれている（意味は後で説明する）。そして第3に、2000年以上の歴史を持つ数学の探求において、これまでに発見された最大の素数である。

発見

この数（略してM136279841として知られる）が素数であるという発見は、10月12日、カリフォルニア州サンノゼ出身の36歳の研究者であるルーク・デュラント (Luke Durant) 氏によってなされた。デュラント氏は、グレート・インターネット・メルセンヌ素数探索 (GIMPS) という、長い間続いている活動に関わっている。数千人のボランティアがGIMPSに参加し、デュラント氏はそのうちの一人である。

2のべき乗（数学者が2^p-1と表記する数）より1少ない素数は、メルセンヌ素数と呼ばれる。350年以上前にこの素数を研究したフランスの修道士であるマリン・メルセンヌにちなんで名づけられた。最初のメルセンヌ素数は3、7、31、127である。

メルセンヌ素数を探す長い旅
メルセンヌ素数は2^p-1の形をしている。最大で数百万桁になるため、実際の数を視覚化することは不可能だが、指数 (2がそれ自身と掛け合わされる回数) をプロットすることはできる

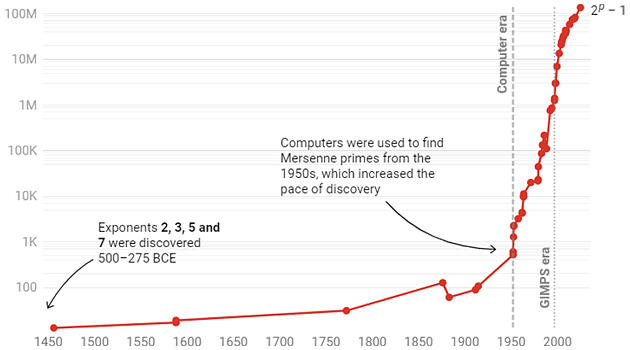
Chart: The Conversation, Source: GIMPSGet the dataCreated with Datawrapper

デュラント氏は、数学的アルゴリズム、実用的なエンジニアリング、そして膨大な計算能力を組み合わせてこの発見をした。今までは従来のコンピュータープロセッサ (CPU) を使用して大きな素数が発見されていたが、今回の発見は、GPUと呼ばれる異なる種類のプロセッサを使用した初めてのこととなる。

GPUはもともと画像や映像の生成を高速化するために設計されたものであるが、最近では暗号通貨のマイニングやAIの強化など、別の使われ方をしている。

デュラント氏は大手GPUメーカーであるNVIDIAの元従業員であり、クラウドで強力なGPUを使用して、17か国にまたがる一種の「クラウドスーパーコンピューター」を作成した。その幸運なGPUは、アイルランドのダブリンにあるNVIDIA A100プロセッサである。

素数と完全数

この進歩は数千年にも遡るストーリーの続きであり、発見の高揚感以上のものがある。数学者がメルセンヌ素数に魅了される理由の1つは、いわゆる「完全」数と結びついていることである。

ある数の真の約数の和をすべて足し合わせるとその数自体になる場合、その数は完全数である。たとえば、6=2×3=1+2+3であるため、6は完全数である。同様に、28=4×7=1+2+4+7+14である。

すべてのメルセンヌ素数には、対応する偶数の完全数もある。(奇数の完全数が存在するかどうかは不明であり、数学における最も古い謎の1つとなっている)。

完全数は歴史を通じて人類を魅了してきた。たとえば、初期のヘブライ人や聖アウグスティヌスは、神が地球を正確に6日間で作った(7日目は休息日)ことから、6を真に完全な数と考えていた。

実用的な素数

素数の研究は、歴史上に見られる好奇心だけの話ではない。数論は現代の暗号にも不可欠である。たとえば、多くのウェブサイトのセキュリティは、大きな数の素因数を見つけることの困難に依存している。

いわゆる公開鍵暗号 (たとえば、ほとんどのオンラインアクティビティを保護する種類のもの) で使用される数は、通常、10進数で数百桁のものであり、M136279841 と比較すると非常に小さい。

それでも、数論の基礎研究（素数の分布の研究、数が素数か否かを調べるアルゴリズムの開発、合成数の因数の検索など）の利点は、多くの場合、下流に影響を与え、デジタル通信におけるプライバシーとセキュリティの維持に役立っている。

終わりのない探索

メルセンヌ素数は実に貴重なものである。この新記録は52番目の発見であり、その前に発見されたメルセンヌ素数より1600万桁以上大きい。

素数は無限に存在することはわかっている。このことは、2000年以上前にギリシャの数学者ユークリッドによって証明された。もし素数が有限個しかなければ、それらをすべて掛け合わせて1つ足すことができる。その結果は、これまでに発見されたどの素数でも割り切れない。ということは、少なくとももう1つは必ず存在することになる。

しかし、メルセンヌ素数が無限に存在するかどうかは分からない。とはいえ、存在すると推測されてはいる。残念ながら、メルセンヌ素数は我々の技術では検出できないほど少ないのである。

今のところ、この新しい素数は、人類の好奇心のマイルストーンとなっており、テクノロジーが支配する時代であっても、数学の世界の深く魅力的な秘密のいくつかは手の届かないままであることを知らしめている。課題は依然として存在し、数学者や愛好家は、数が持つ無限のタペストリーに隠されたパターンを見つけようとしている。

そして、完全を求める（数学的）探索はこれからも続くことであろう。

（2024年12月4日公開）

著者：John Voight（シドニー大学 数学科教授）

原文記事(外部サイト)：
A 41-million-digit prime number is the biggest ever found — but mathematicians' search for perfection will continue

本記事は、2024年11月14日にThe Conversationに掲載後、著者の許諾を得て再構成したものです。掲載された記事、写真の無断転載を禁じます。